Die Kapitalmärkte sind „eigentlich“ ganz einfach und sehr effizient, da sich die Preise fortlaufend durch Angebot und Nachfrage bilden. Gleichzeitig liegt ihnen eine enorme Komplexität zugrunde, die kein Mensch jemals wirklich durchschauen kann. Deshalb sind die Märkte gleichzeitig auch so kompliziert.
Das gleiche gilt für Renditeberechnungen: Auf den ersten Blick ganz einfach, aber im Detail dann doch kompliziert.
Nachdem ich vor einer Weile schon drei andere „Gesetze“ an den Märkten vorgestellt habe, möchte ich diese nun um die Kosten der Volatilität, den sogenannten Volatility Drag, ergänzen. Ich nehme dabei den DAX als Beispiel, da damit jeder etwas anfangen kann.
Die arithmetische Rendite
Im einfachsten Fall ist die Rendite gemeint, die über einen bestimmten Zeitraum erzielt wurde. Beim DAX betrug diese im letzten Jahr 25,48%. So einfach kann die Börse sein. Aber wir sind noch nicht ganz fertig.
Wenn wir den DAX über viele Jahre betrachten, können wir eine Durchschnittsrendite pro Jahr errechnen. In den 30 Jahren von 1990 bis 2019 erzielte er Jahresrenditen zwischen -40,37% (2008) und 46,7% (1993). Als Durchschnitt der einzelnen Jahresrenditen ergeben sich 9,67%.
Die geometrische Rendite
Allerdings ist dieser arithmetische Durchschnitt nicht das, was der DAX wirklich als jährliche Wachstumsrate erzielte. Denn wenn wir den Startwert zum Jahresende 1989 nehmen (1790,37 Punkte) und die durchschnittliche jährliche Rendite ermitteln, um im Dezember 2019 beim Endwert (13.249,01 Punkte) zu landen, kommen wir „nur“ auf 6,90 Prozent. Das ist die wahre, geometrische Durchschnittsrendite unter Annahme einer jährlich konstanten Kurssteigerung.
Der Unterschied zwischen arithmetischer und geometrischer Rendite kommt durch die Volatilität der Kurse zustande. Je höher diese ist, desto größer die Differenz. Das lässt sich anhand eines extremen Beispiels gut zeigen: Würde der Markt in einem Jahr um 50 Prozent fallen und im nächsten Jahr um 100 Prozent steigen, läge die arithmetische Rendite bei 25 Prozent (Berechnung: (-50% + 100%) / 2), aber die geometrische Rendite bei 0 Prozent. „Richtig“ für Investments ist aber nur die geometrische Rendite, da sich der Index nach einem Kursverlust von 50 Prozent und einem Wiederanstieg um 100 Prozent per Saldo nicht bewegt hat.
Der Volatility Drag
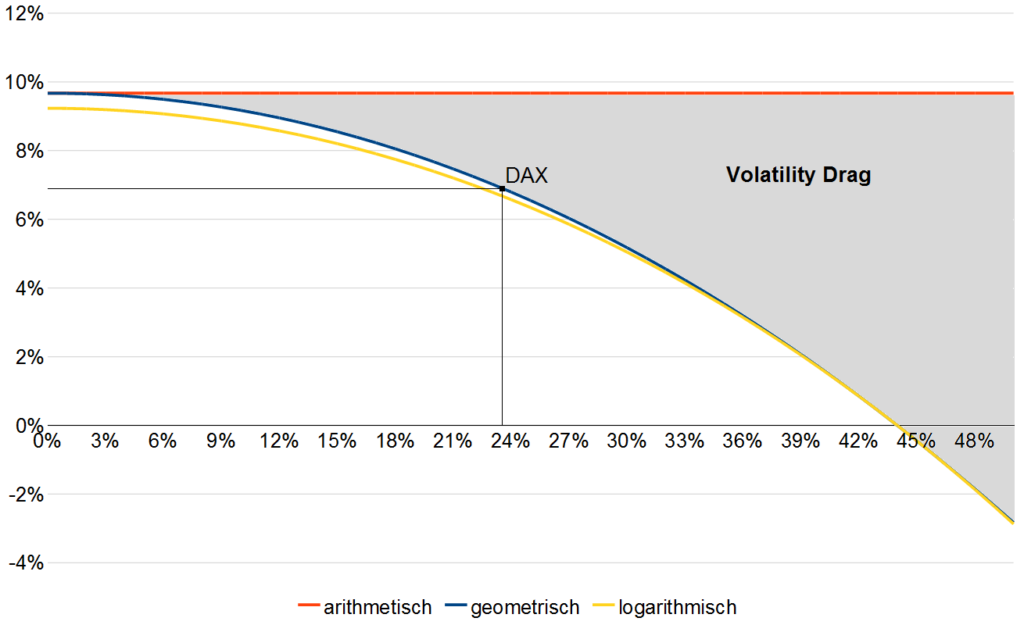
Wie gerade gezeigt sollte man nur der langfristigen, geometrischen Rendite eines Investments vertrauen. Das gilt umso mehr, je höher die Volatilität und die damit verbundenen Kosten sind, was auch als Volatility Drag bezeichnet wird.
Es gibt eine einfache, approximative Formel, um den Volatility Drag zu berechnen. Dazu brauchen wir die Standardabweichung der einzelnen Renditen. Diese beträgt für unser DAX-Beispiel, wenn wir die 30 einzelnen Jahresrenditen zugrunde legen, 23,42 Prozent. Die Formel lautet:
Volatility Drag = Standardabweichung * Standardabweichung / 2
Für unsere Werte also: 23,42% * 23,42% / 2 = 2,74%
Mithilfe dieses Werts können wir nun aus der arithmetischen die geometrische Rendite ermitteln:
geometrische Rendite = arithmetische Rendite – Volatility Drag
Für unsere Werte also: 9,67% – 2,74 = 6,93%
Wie von Zauberhand haben wir auf diese Weise auf die erste Nachkommastelle genau die geometrische Rendite indirekt aus arithmetischer Durchschnittsrendite und Standardabweichung geschätzt. Die Abweichung zur oben berechneten, tatsächlichen geometrischen Rendite beträgt nur 0,03 Prozent.
So weit, so gut. Das beste kommt aber noch.
Die logarithmische Rendite
Die Log-Rendite ist ein finanzmathematisches Konstrukt, das wir schon aus der Schule unter dem Begriff der stetigen Rendite kennengelernt haben. Erinnern wir uns, wie der Lehrer damals sagte, dass wir all das irgendwann in unserem Leben einmal brauchen werden 🙂
Diese Zeit ist jetzt gekommen. Denn mit der Log-Rendite können wir uns das gerade beschriebene Hin und Her zwischen arithmetischer und geometrischer Rendite ersparen. Indem wir die Renditen von Vornherein logarithmieren und damit verstetigen, bekommen wir die Rendite, die wir bei „unendlich schneller“ fortlaufender Verzinsung erhalten.
Man könnte jetzt viel rund um die Euler’sche Zahl schreiben, aber ich möchte es so einfach wie möglich halten. Deshalb wieder ein einfaches Beispiel anhand der DAX-Rendite des Jahres 2019, die wie eingangs genannt 25,48 Prozent betrug. Die logarithmische Rendite dazu ist 22,69 Prozent (Berechnung: LN (1,2548)).
Was bedeutet das nun? Ganz einfach: Wenn wir mit einer Rendite von Sekundenbruchteil zu Sekundenbruchteil von 22,69 Prozent im Jahr rechnen, also einen „unendlichen“ Zinseszinseffekt haben, kommen wir am Ende des Jahres bei 25,48 Prozent einmaliger Jahresrendite heraus.
Umgekehrt ist es leider bei negativen Renditen. Nehmen wir das Jahr 2018 als Beispiel, so lag die DAX-Rendite bei -18,26 Prozent, was einer Log-Rendite von -20,16 Prozent entspricht. Dieser Effekt, dass die positiven Log-Renditen kleiner sind und die negativen Log-Renditen größer im Minus liegen, führt zu einer annähernden Normalverteilung der Renditen im Zeitablauf – anders als die arithmetischen Renditen, deren Verteilung deutlich verzerrt ist.
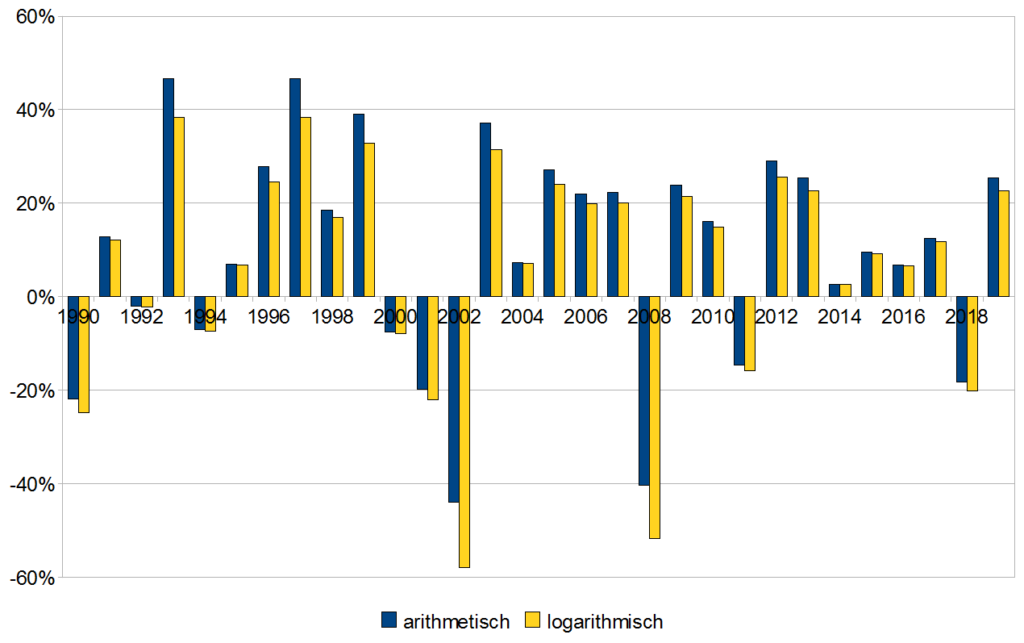
Aber zurück zum Beispiel: Wenn wir nun alle unsere 30 DAX-Jahresrenditen logarithmieren und deren Durchschnitt berechnen, kommen wir auf ein erstaunliches Ergebnis von 6,67 Prozent. Das entspricht genau der Log-Rendite unserer oben berechneten geometrischen DAX-Rendite von 6,90 Prozent (Berechnung: LN (1,0690)).
Mit anderen Worten: In den letzten 30 Jahren erzielte der DAX eine stetige Rendite, also einen „permanenten Zins“ von 6,67 Prozent. Aufs Jahr gerechnet entspricht das einer echten Durchschnittsrendite von 6,90 Prozent.
Fazit
Die geometrische Jahresrendite ist auf Dauer die wahre Rendite, die wir bei einem Investment unter Berücksichtigung seiner Volatilität erzielen.
Danke für diesen schönen Artikel. Verständlich und klar erklärt. Gerade, wenn einem Fondsangebote mit vermeintlich toller Rendite unterbreitet werden, sollten Anleger da ruhig Mal genauer hinsehen, von welcher Rendite hier eigentlich gesprochen wird. 😉
Super Beitrag! Jetzt hab sogar ich als Blondine das verstanden 😀
Danke! Habe jetzt noch eine zweite Grafik hinzugefügt, die den Zusammenhang anschaulich visualisiert.
Ein erhellender Artikel, allerdings wäre die Verwendung des DAX Kurs- statt des allseits bekannten Performance-Index nach meinem Dafürhalten noch besser gewesen, da dies zusätzlich deutlich gemacht hätte, wie mäßig der Erfolg des deutschen Marktes gegenüber dem US-Markt ist.
Danke. Für den Effekt im Beispiel spielt die relative Performance gegenüber anderen Märkten keine Rolle.